Reise nach Jerusalem
Zuordnungen a la Gerhard Schmeisser
Professor Gerhard Schmeisser hat vorgeschlagen, die Zuordnungen der
Nullstellen eines Polynoms zu denen seiner Ableitung über Polynome
zu machen, deren Koeffizienten sich stetig ändern. Für
jedes lambda zwischen 0 und 1 wird das Polynom
f_lambda = (1-lambda)*f + lambda*f'
betrachtet. lambda=0 gibt das ursprüngliche Polynom f (vom Grad n),
und
bei lambda=1 ist man bei der Ableitung f' angelangt. Die Nullstellen
von f_lambda ändern sich stetig mit lambda. Für alle lambda < 1
hat f_lambda den gleichen Grad n wie f, also auch genau so viele Nullstellen.
f_lambda ist auch für alle anderen lambda ungleich 1 (also solche
> 1 und solche < 0) ein Polynom vom Grad n. In den folgenden Diagrammen
sind die Nullstellen für alle f_lambda zwischen -3 und +1 angezeigt.
Dunkelblaue Punkte sind die Nullstellen von f selbst. Rote Kreuzchen
markieren die Nullstellen der Ableitung f'. In allen Diagrammen der
ersten Serie hat f fünf Nullstellen, nämlich -2, -1, +1, +2
und die fünfte Nullstelle bei p*i (also rein imaginär) für
reelle Werte p zwischen 1 und 2.
Das Programm zur Berechnung aller Nullstellen und für die
Visualisierung hat im Sommer 2013 der sehr kompetente Student
Patrick Wieschollek geschrieben. Ihm gilt mein Dank
dafür!
Polynom vom Grad 5 mit einer variablen Nullstelle
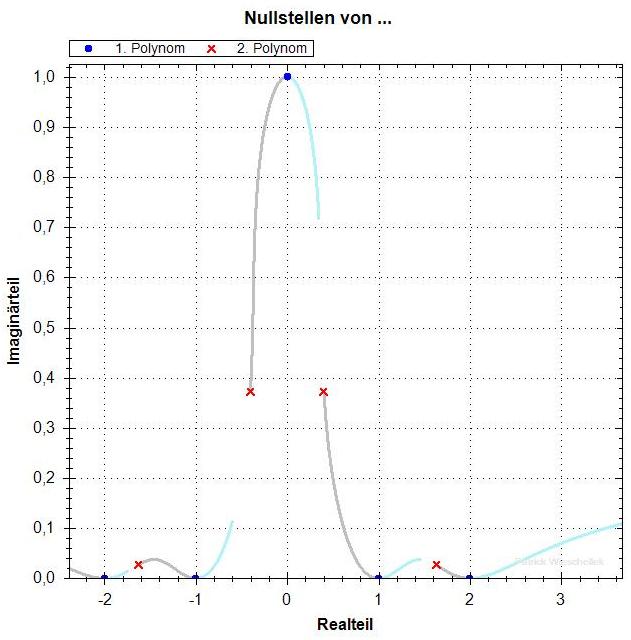
p=1.00
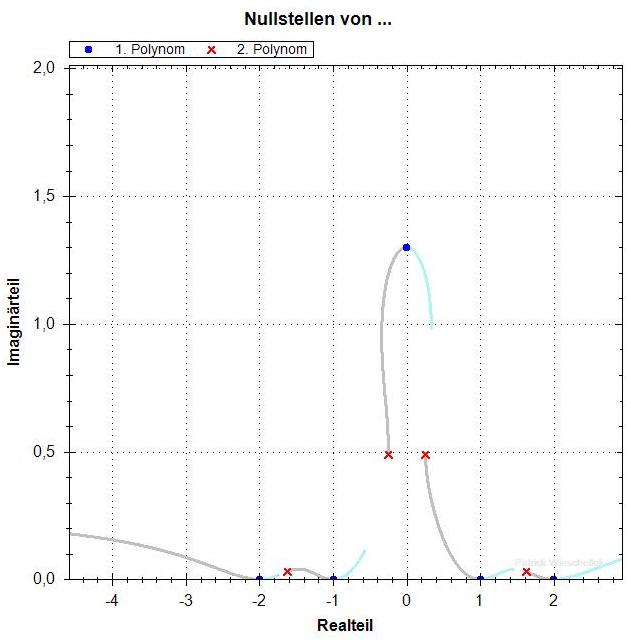
p=1.30
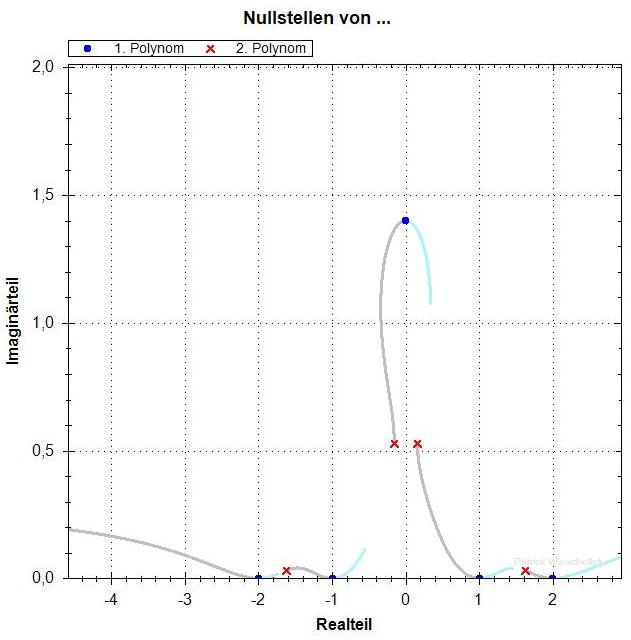
p=1.40
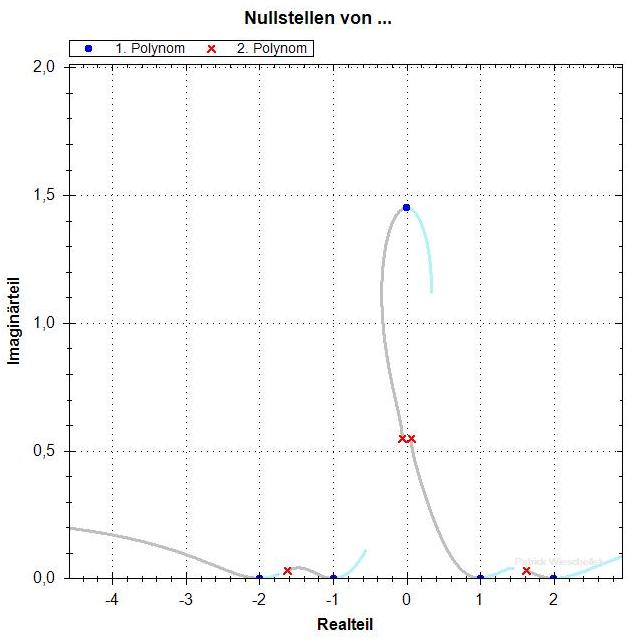
p=1.45
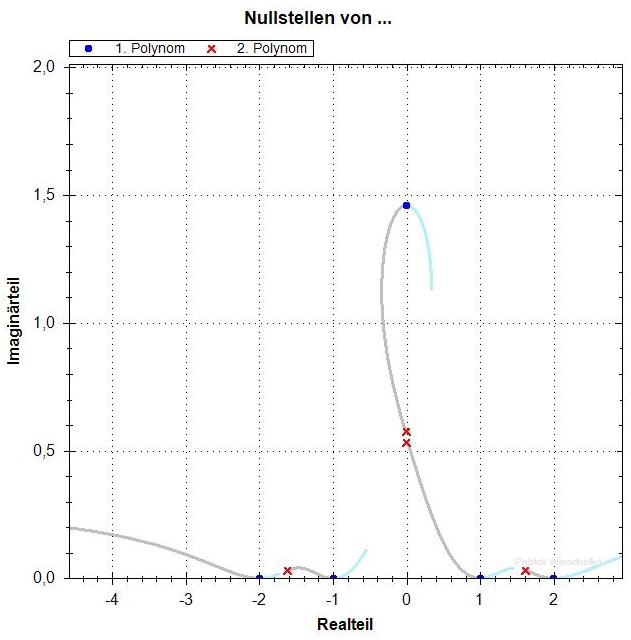
p=1.46
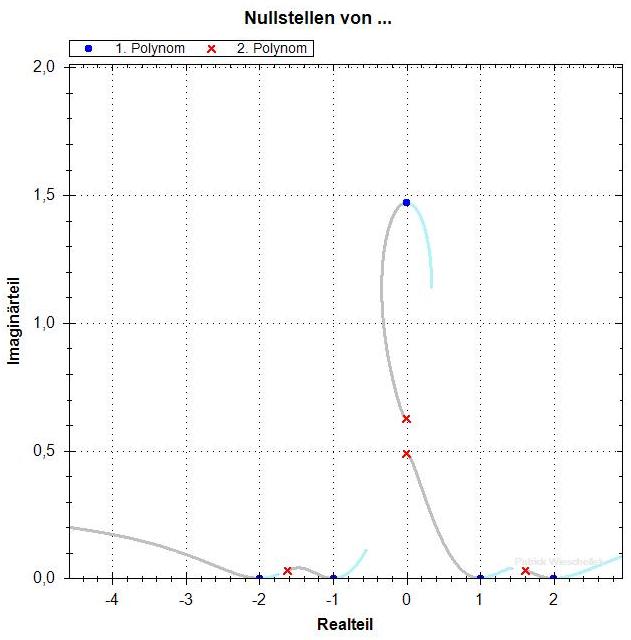
p=1.47
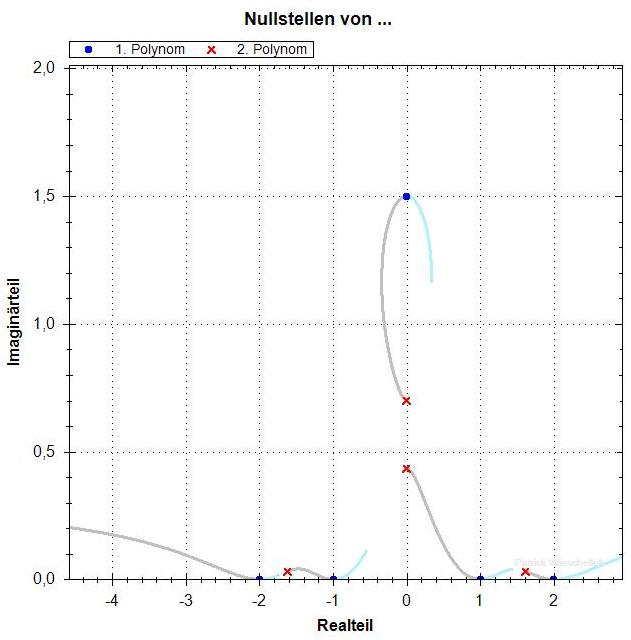
p=1.50
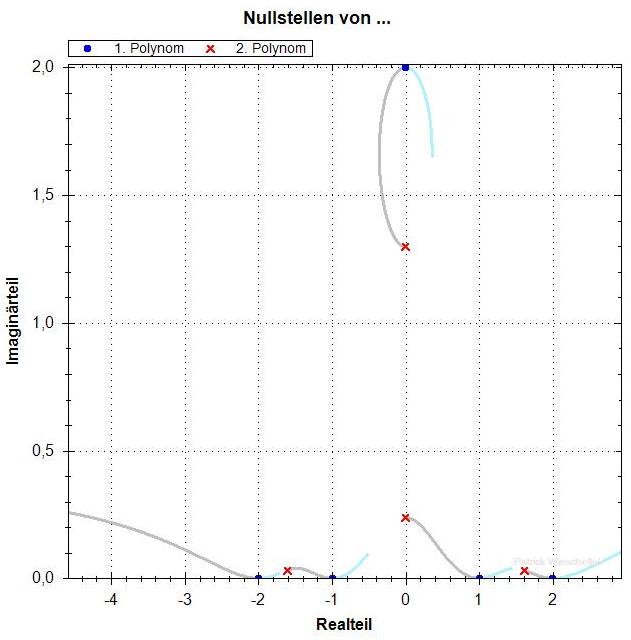
p=2.00
Die Nullstellen von f' hängen stetig von p ab. Bis p = 1.45
gibt es zwei Nullstellen mit deutlich positivem Imaginärteil,
die nebeneinander liegen. Dann, für p > 1.45, "läuft die
eine nach oben weg" und die andere sackt nach unten ab. An der
gleichen Stelle (nahe p=1.45) ändert sich die Struktur der
Kurven aus den f_lambda-Nullstellen. Für kleinere p sieht man,
dass es insgesamt einen Pfad gibt, der durch alle Nullstellen von
f und f' geht. Für die grossen p hat sich aber ein "Zykel"
mit nur einer f- und einer f'-Nullstelle nach oben abgespalten.
Ein Polynom vom Grad 16
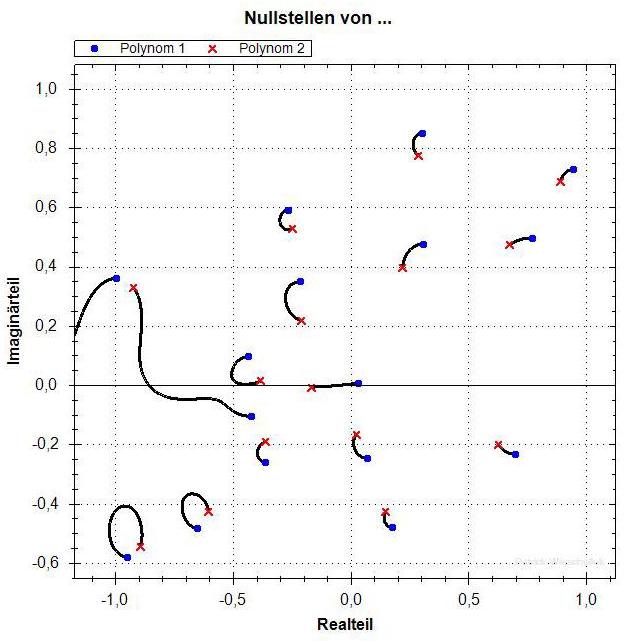
Eingezeichnet sind nur die Nullstellen der f_lambda
für lambda zwischen 0 und 1.
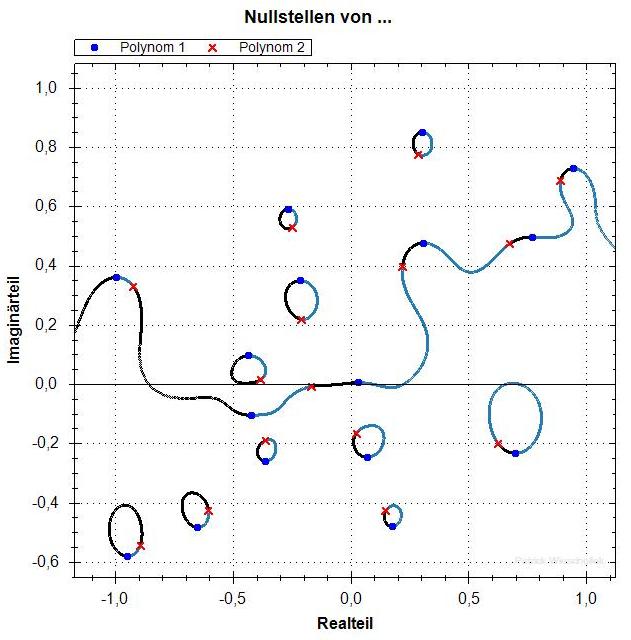
Jetzt sind die Nullstellen für alle lambda zwischen
-10 und +11 zu sehen. Die hellblauen Punkte gehören
zu Nullstellen für Lambda-Werte ausserhalb von [0,1].
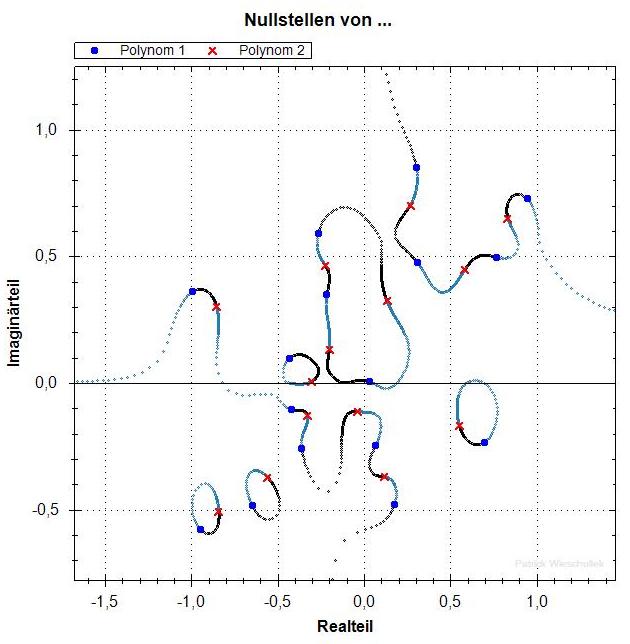
Hier sind nicht f und f' konvexkombiniert, sondern f und
ihre zweite Ableitung f''. Weil bei f'' also zwei Nullstellen
gegenüber f "fehlen", gibt es zwei Fäden, die
ins Unendliche laufen.
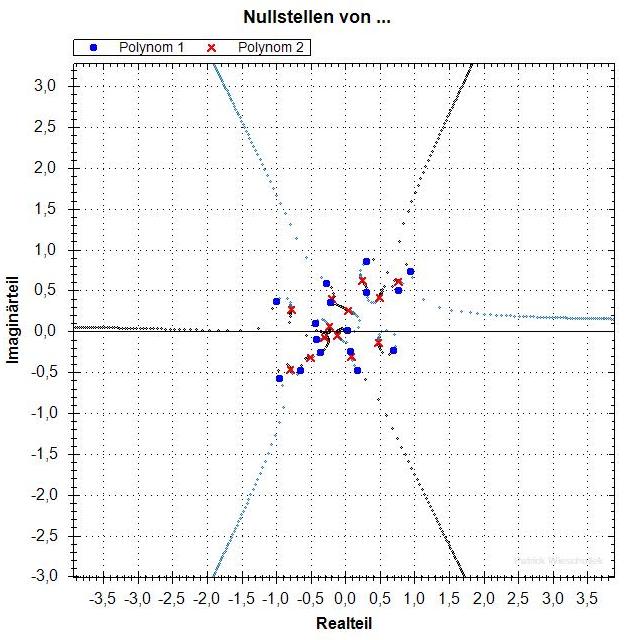
Für f und die dritte Ableitung f''' habe ich einen
gröberen Mass-Stab gewählt. So sieht man besser,
wohin die insgesamt drei offenen Fäden ins Unendliche
laufen.
Noch ein Polynom vom Grad 5
Das Polynom hat die vier Nullstellen 0, 2, 3+i und 4.
Zusätzlich hat es eine weitere Nullstelle mit Realteil 0
und positivem Imaginärteil q. Je nach der Grösse
von q ergibt sich ein anderer Verlauf der Nullstellen-Kurve(n).
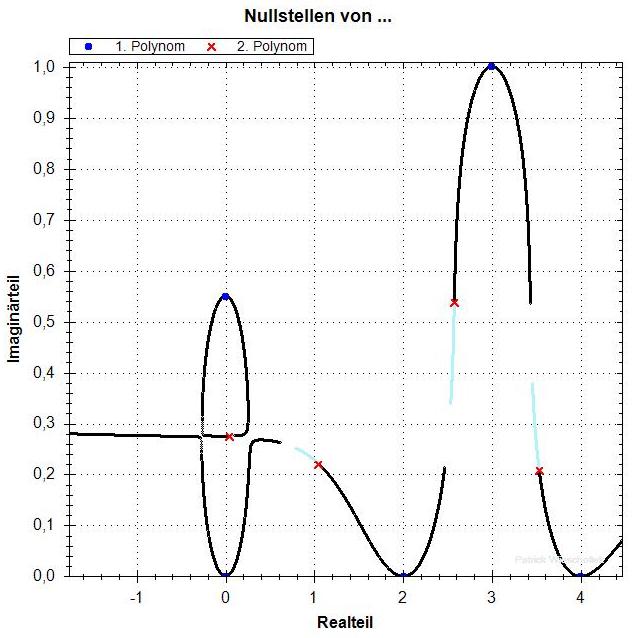
q=0.55 .
Bei Realteil 0 gibt es oben einen kleinen Zyklus.
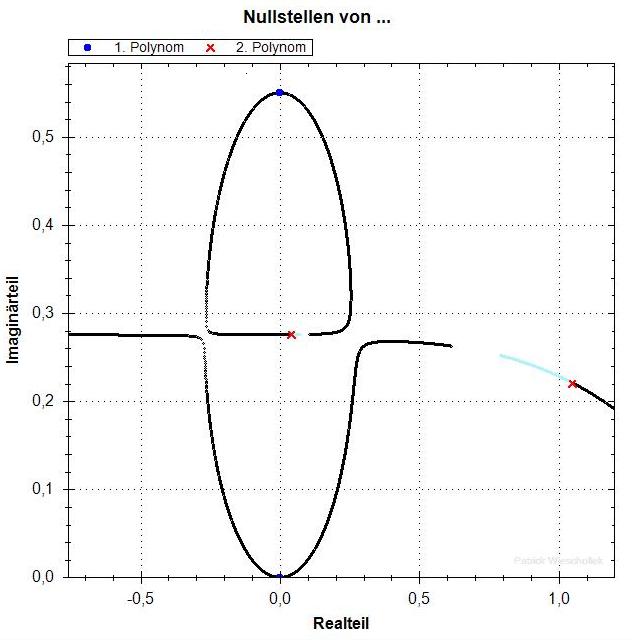
Noch einmal q=0.55 .
Hier ist der interessante Teil in Vergrösserung gezeigt.
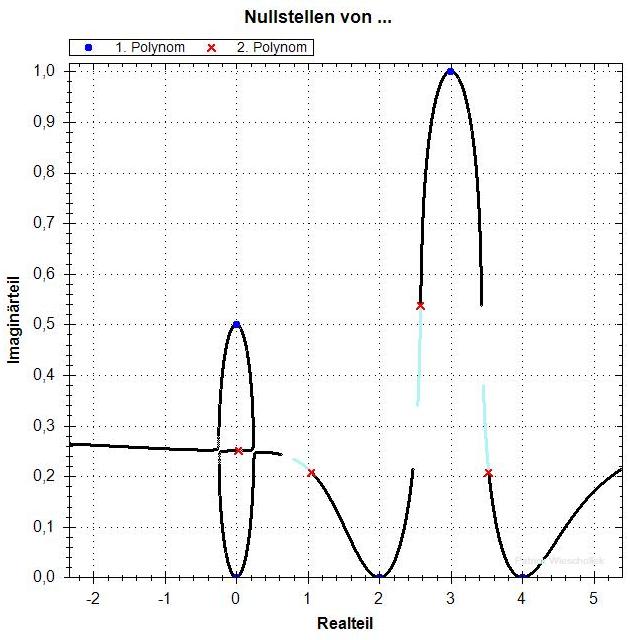
Jetzt ist q=0.50 .
Insgesamt gibt es nur eine Kurve, die alle Nullstellen von
f und f' enthält.
Bei Realteil 0 macht die Kurve einen tollen S-Schlenker.
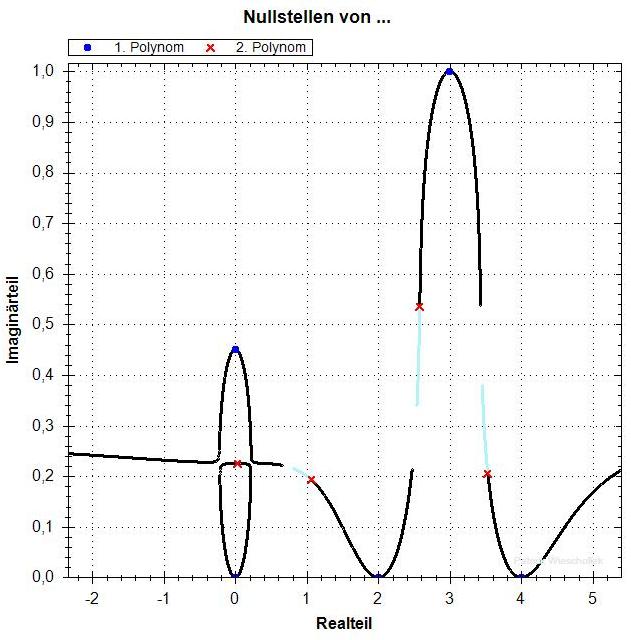
Jetzt ist q=0.46 .
Wieder gibt es bei Realteil 0 einen kleinen Zyklus. Diesmal
enthält er aber die untere der beiden Nullstellen.
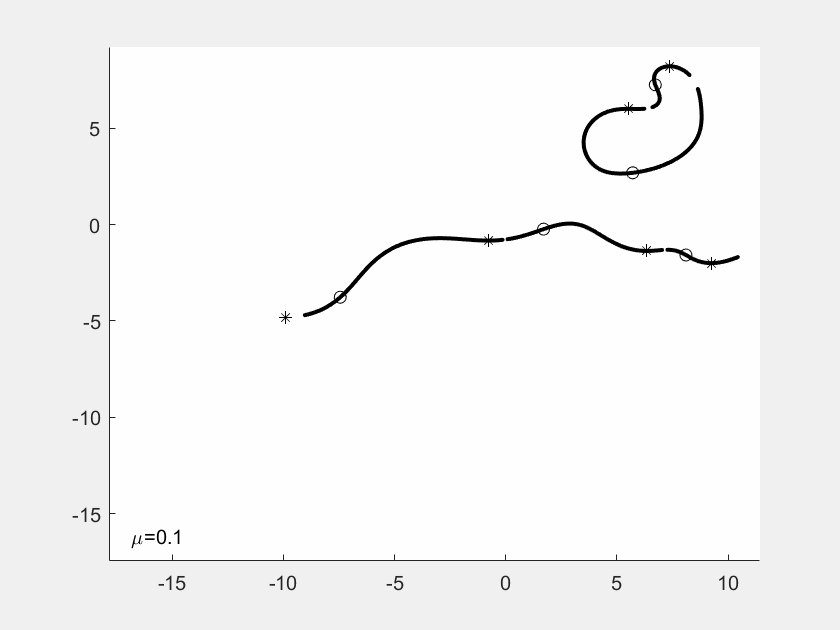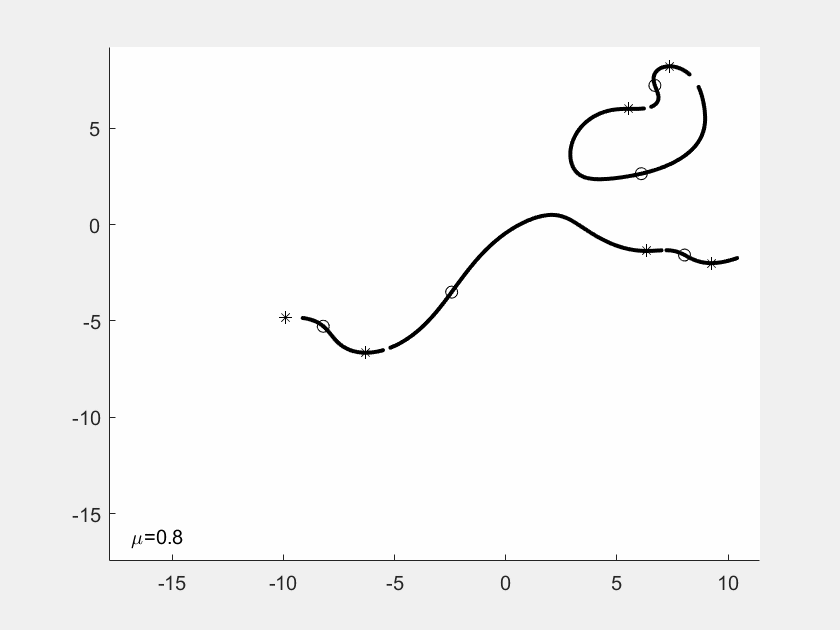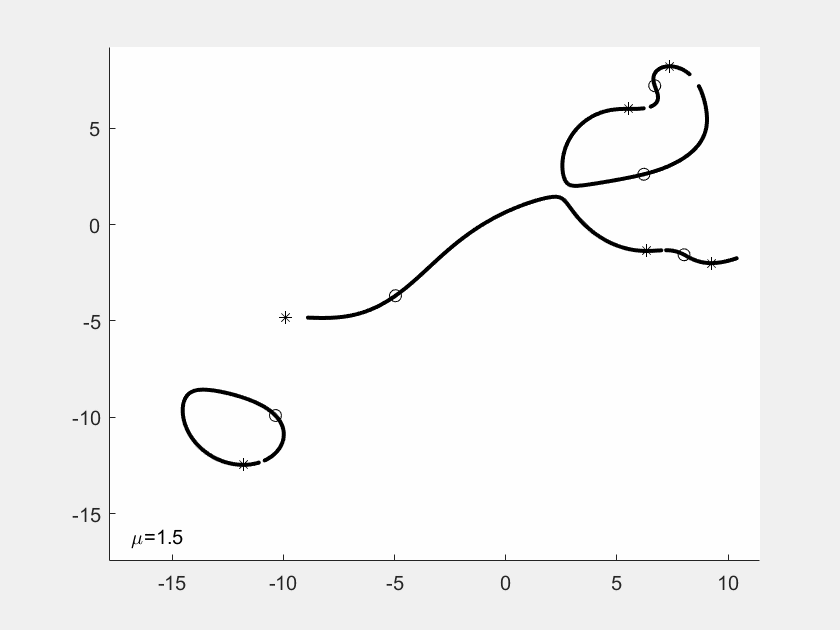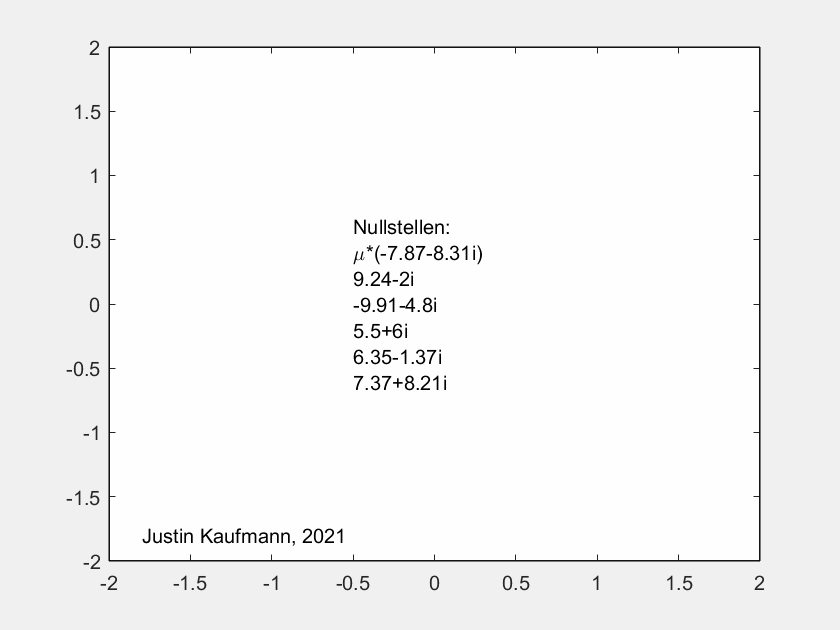
GIF-Filme von Justin Kaufmann
In seiner Masterarbeit hat Justin Kaufmann 2021
kleine GIF-Filme erzeugt. Jedes Einzelbild zeigt die Kurven
zu Nullstellen und Ableitungs-Nullstellen, wobei von Bild
zu Bild eine der f-Nullstellen wandert, ausgelöst durch einen
Faktor mü vor der Nullstelle. Man sieht an der Sequenz, wie
sich die Gebilde eigentlich stetig ändern, aber mit gelegentlichen
Sprungstellen.
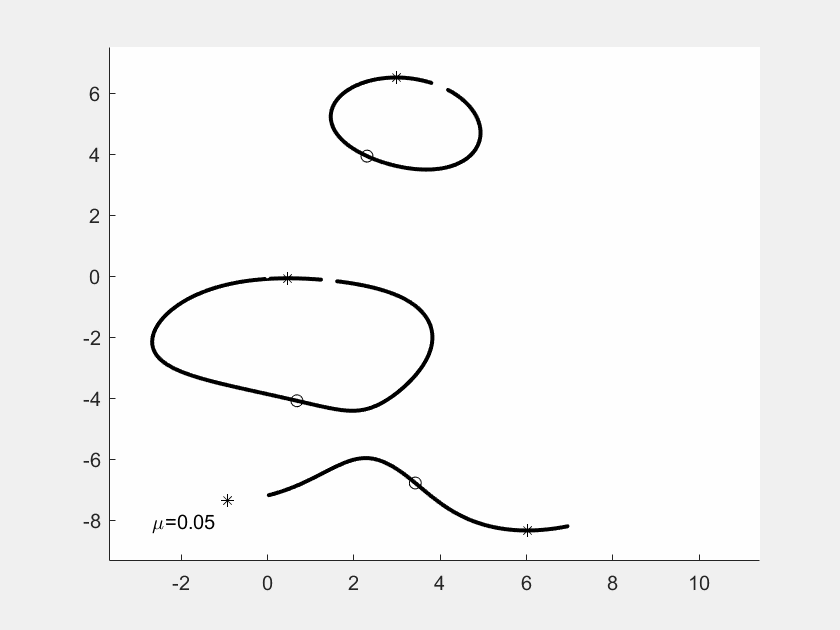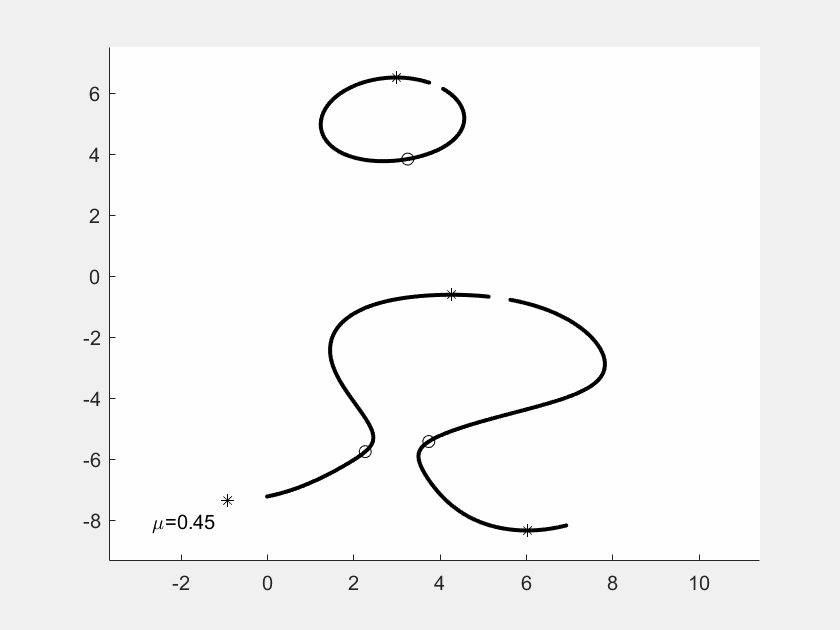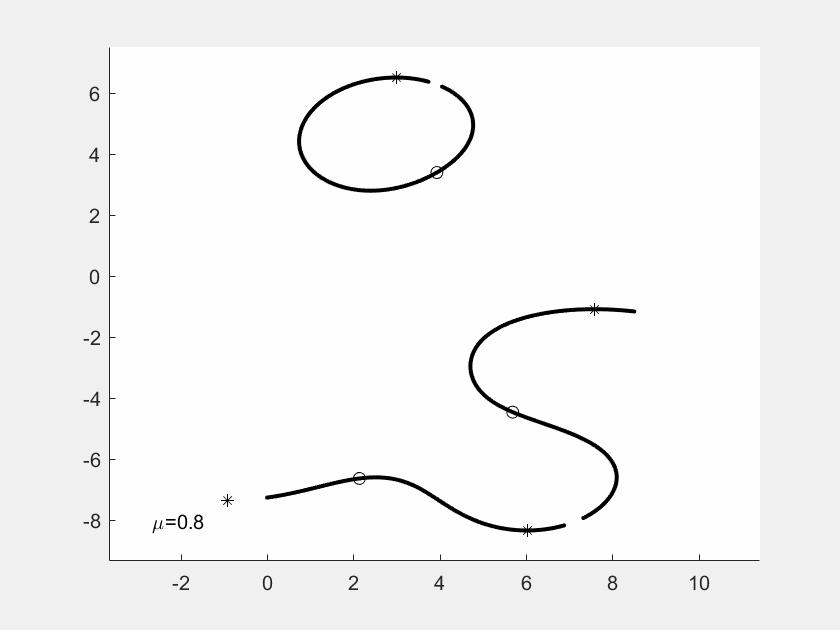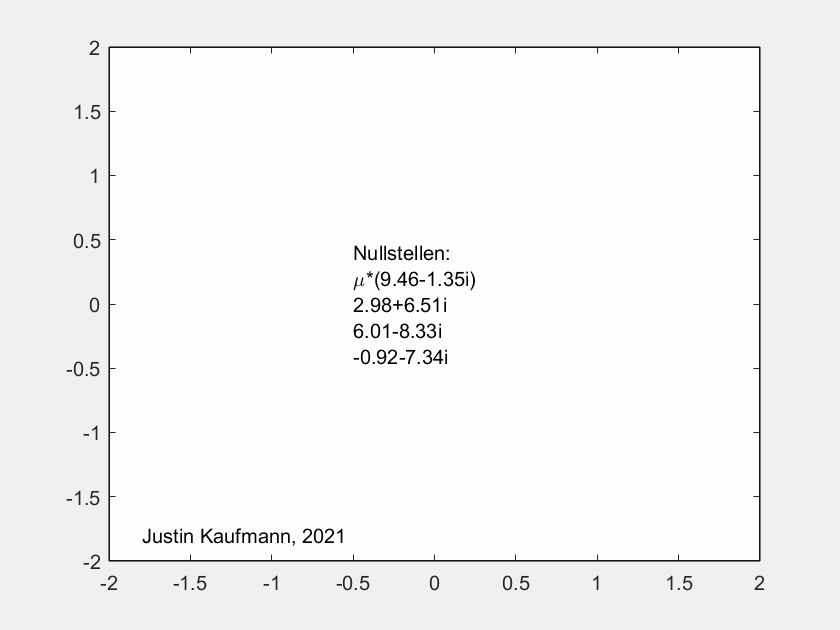
In diesem Beispiel hat f Grad 4. Die vier f-Nullstellen sind
durch Sternchen markiert, die Nullstellen von f' duch Kuller.
Am Ende der Sequenz sind die Nullstellen explizit als Dezimalzahlen
angegeben.
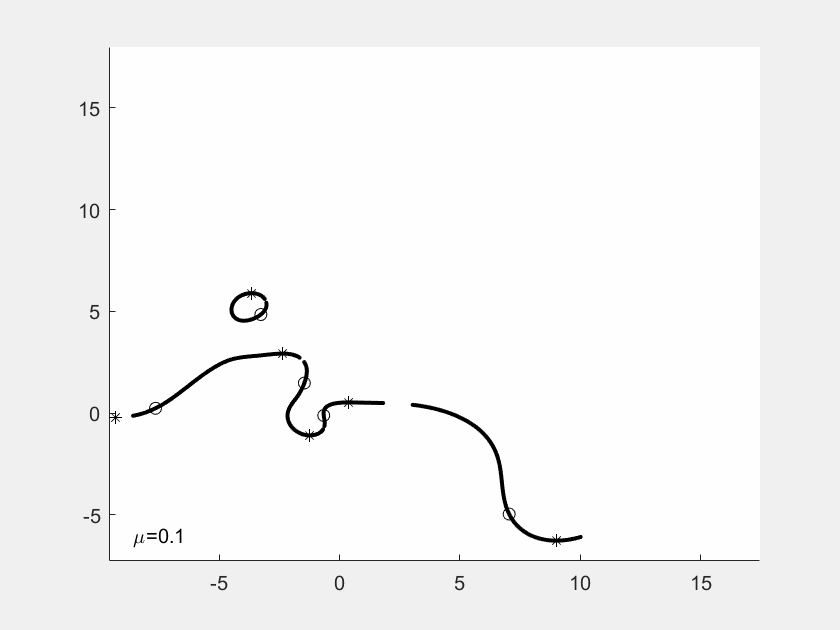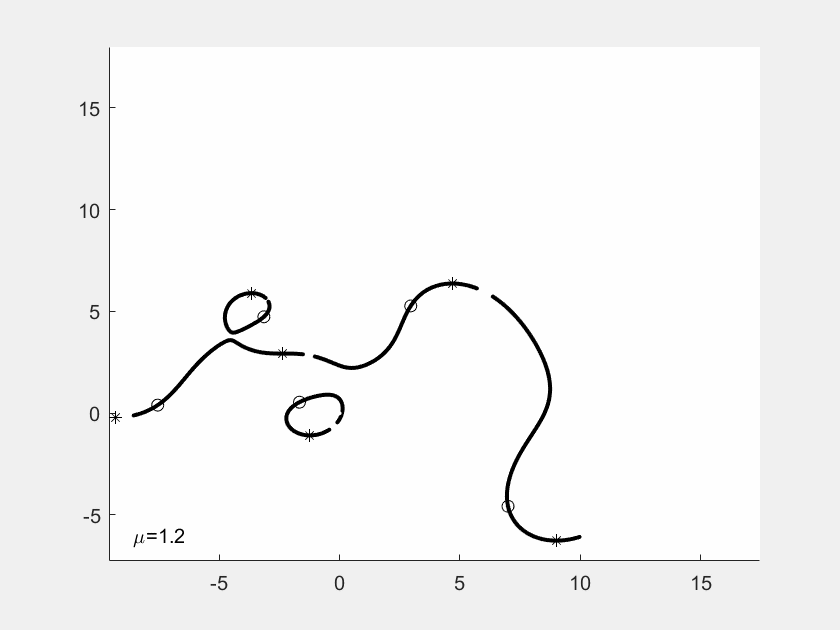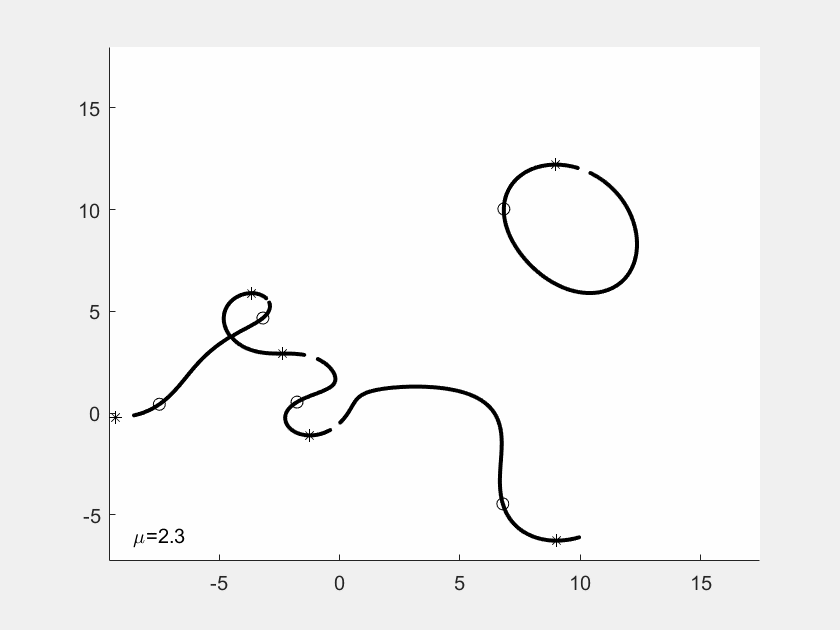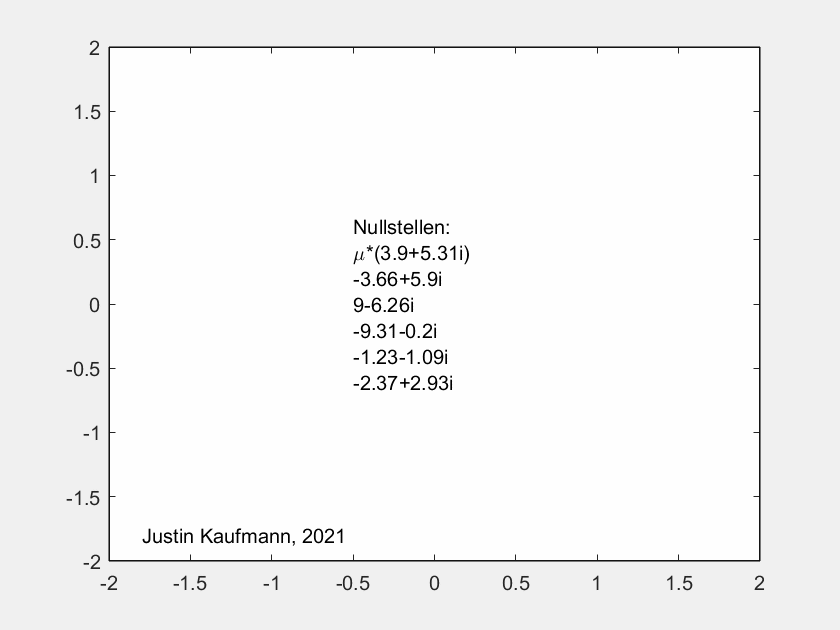
Das erste Beispiel für ein Polynom vom Grad 6.
Das zweite Beispiel für ein Polynom vom Grad 6.
Zurück zur Buchseite


















