Exotic Structures of LEGO Bricks
by Ingo Althöfer, March 05, 2014; Update March 11, 2014;
Disclaimer: LEGO is a trademark of the LEGO Group.
My investigations on exotic structures are neither sponsored
nor supported nor authorized by the LEGO group.
Danish mathematicians Mikkel Abrahamsen and Soren Eilers have written
a very nice paper, entitled "On the Asymptotic Enumeration of
LEGO Structures". It was published in the journal
Experimental Mathematics 20 (2011), 145-152.
Their formal definition of "contiguous structure" does not include the
"exotic" (topologically non-trivial) examples shown on this site.
Chain-Like Structures

The building blocks/rings.

Two rings intertwined.

Three rings intertwined.
Ring around a Bone


Bricks in a Chamber

Open chamber.

Closed chamber.


Observe that the two structures with two bricks in the closed chamber
can not be smoothly converted into another.


Observe that the two structures with three bricks in the closed chamber
can not be smoothly converted into another.
*** Conjectures ***
1. Almost all (contiguous) large structures are NOT simply connected.
Here "simply connected" is meant in the topological sense.
An example: Building random planar structures from 1x3-bricks
step by step
(with equal distribution for the "docking" places of each new brick)
results in a first hole after typically 6 to 30 bricks. The collage
below shows a case where the first hole occured with the tenth brick.

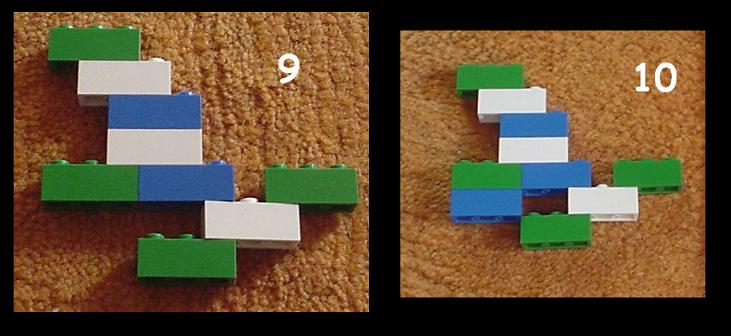
2. Almost all (contiguous) large structures have many "nice" handles.
Here, "nice" is meant with respect to our intention to couple
two (or more) structures together like in the chain-structure photos
on top of this site. Observe that not all handles in LEGO structures
allow chain-like connections. The blue structure in the next
photo is a simple example of a bad handle.

3. Almost all large structures are not contiguous structures in the spirit
of Abrahamsen and Eilers.
When two structures with nice handles are given, they can be in
coupled state.
The more nice handles the structures have, the more likely it is
that they will occur in coupled state.

These conjectures are meant also for (3-dimensional) structures
which are made of 4x2-bricks only.
Back to the main site of Ingo Althöfer
Zurück zur Hauptseite von Ingo Althöfer